什么是谐振子:框图及其类型

简单的谐波运动由法国数学家Baron Jean Baptiste Joseph Fourier于1822年发明。Edwin Armstrong（1954年12月18日至2月1日）在1992年观察到了1992年的振荡，并在他们的实验和亚历山大·梅斯纳（1958年1月14日至1958年1月3日）发明振子1993年3月。“调和”这个词是一个拉丁词。本文概述了谐振子的定义、类型及其应用。

什么是谐振子?

谐振子被定义为一种运动，其中的力与平衡点的粒子成正比，它产生正弦波形的输出。引起谐波的力运动可以在数学上表达为

F = kx

哪里，

恢复力

k =弹簧常数

x =距离平衡的距离

在简谐运动中，有一个点使系统振荡，这个力使质量一次又一次地从它开始的同一点，这个力叫做恢复力，这个点叫做平衡点或平均位置。这个振荡器也被称为a线性谐波振荡器。能量来自于活动组件在振荡器中的被动组件。

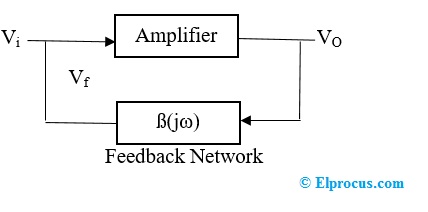
框图

该谐振子的框图由组成一个放大器和反馈网络。放大器用于放大信号，并且该放大信号通过反馈网络并产生输出。其中VI是输入电压，VO是输出电压，VF是反馈电压。

例子

春天的质量：弹簧提供加速质量的恢复力，并且恢复力表示为

f = ma.

其中'm'是质量，a是加速度。

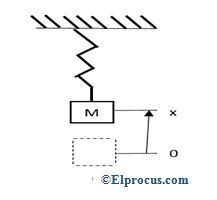
春天由质量（m）和力（f）组成。当力在点X = 0处拉动质量并且仅取决于x - 质量的位置，弹簧常数由字母k表示。

谐振子的类型

该振荡器的类型主要包括以下几种。

强制谐波振荡器

当我们对系统的运动施加外力时，这个运动就称为受迫谐振子。

阻尼谐波振荡器

这个振子被定义为，当我们对系统施加外力时，振子的运动减少，它的运动被称为阻尼谐运动。阻尼谐振子有三种类型

过度潮湿

当系统缓慢地向平衡点移动时，就称为过阻尼谐振子。

在潮湿下

当系统快速朝向平衡点移动时，据说据说是一个覆盖的谐波振荡器。

临界阻尼

当系统在不围绕平衡点振荡的情况下尽可能快地运动时，就称为过阻尼谐振子。

量子

它是由哥廷根大学的马克斯·博恩、维尔纳·海森堡和沃尔夫冈·泡利发明的。量子这个词是拉丁词，量子的意思是少量的能量。

零点能量

零点能量也称为地位能量。它是定义的，当地面能量总是大于零时，通过Max Planck在德国和1990年开发的公式发现这个概念。

阻尼简谐振子方程的平均能量

有两种类型的能量，它们是动能和势能。动能和势能的总和等于总能量。

E = K+U ...................Eq (1)

这里E =总能量

K =动能

U =潜在的能量

这里k = k = 1/ 2mv²............ eq（2）

U = 1/ 2kx²............ eq (3)

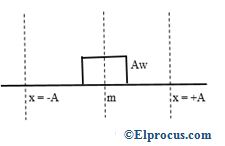
每个振荡周期的动能和势能的平均值等于

哪里V.²= w²(一个²- x²）......EQ（4）

将eq(4)代入eq(2)， eq(3)得到

k = 1/2 m [w²(一个²- x²)]

= 1/2 m [aw cos（wt +Ø_0.)]²……eq (5)

U = 1/ 2kx²

= 1/2 k(罪(wt +ø_0.)]²……eq (6)

替代EQ（5）和EQ（6）在EQ（1）中将获得总能量值

E = 1/2 m [w²(一个²- x²）] + 1/2 kx²

= 1/2 m w²1/2 m w²一种²+ 1/2 kx²

= 1/2 m w²一种²+ 1/2倍²（K-MW²）......EQ（7）

哪里兆瓦²= K，将该值代入eq(7)

e = 1/2 k a²- 1/2 Kx²+ 1/2 x²= 1/2 K A²

总能量（e）= 1/2 k a²

一个时间段的平均能量表示为

K._Avg.= U_Avg.= 1/2（1/2 k a²）

谐振子波函数

哈密顿算符被表示为动能和势能的总和，它被表示为

ђ（q）= t + v .................. .eq（1）

ђ= Hamitonian运营商在哪里

T =动能

势能

要生成波函数，我们必须知道Schrodinger方程，并且等式表示为

——ђ²/ 2μ* d²ѱ_υ（q）/ dq²+ 1 / 2kq²ѱ_υ(问)= E_υѱ_υ(问 ).............eq (2)

其中q =正常坐标长度

μ=有效质量

k =力常数

薛定谔方程边界条件为:

ѱ（ - ∞）=Ø

Ѱ(+∞)= 0

我们也可以把eq(2)写成

D.²ѱ_υ（q）/ dq²+ 2μ/ђ²(E_υ-k / 2 * q²）ѱ_υ（q）= 0 ............ eq（3）

用于求解方程的参数为

β=ђ/√μk......... eq（4）

D.²/ dq.²= 1 /β²D.²/ dx.²..............eq (5)

将eq(4)和eq(5)代入eq(3)，则该振子的微分方程为

D.²ѱ_υ（q）/ dx²+(2μβ²E._υ/ђ²- x²）ѱ_υ（x）= 0 .........。eq（6）

幂级数的一般表达式是

Σc-nx2............。EQ（7）

指数函数表示为

exp（-x.²/ 2 ) ............ eq (8)

EQ（7）乘以EQ（8）

ѱυ（x）=Σc-nx2exp（-x2 / 2）............... ..eq（9）

通过使用以下等式获得Hermite多项式

ђ_υ（x）=（-1）^υ* exp (x²) d / dx^υ* exp (- x²）............... eq（10）

归一化常数表示为

N_υ= (1/2^υυ！√π）^1/2............... .eq（11）

该简单的谐波振荡器解决方案表示为

ѱ_υ（x）= n_υH_υ（y）e^-x2/2.................. eq（12）

其中n_υ为归一化常数

H_υ是埃尔米特

E.^{x2 /2}是高斯

方程(12)是谐振子的波函数。

该表显示了最低能量状态的第一项Hermite多项式

υ	0.	1	2	3.
Hυ（y）	1	2Y.	4Y.22	8 y3.-12 y

波浪功能简谐振子图对于以下四个能量状态如下图所示。

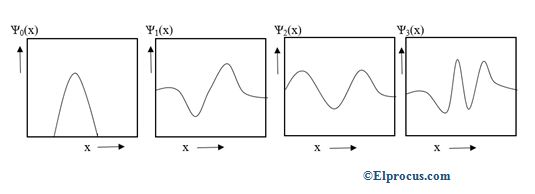
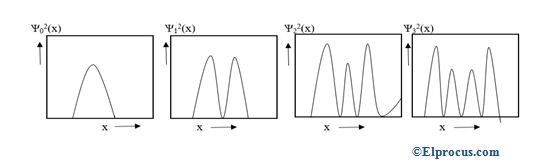
该振荡器对于四个最低能量状态的概率密度在下面的图中示出。

应用程序

S.及其谐振子应用主要包括以下几个方面

• 音频和视频系统
• 无线电和其他通信设备
• 逆变器，警报
• 蜂鸣器
• 装饰照明

优势

该谐振子的优点是

• 便宜的
• 高频发电
• 效率高
• 便宜的
• 便携式
• 经济

例子

这个振荡器的示例包括以下内容。

• 乐器
• 单摆
• 群众弹簧系统
• 摇摆
• 钟指针的运动
• 汽车、卡车、公共汽车等车轮的运动

它是一种运动，我们可以在我们的日常基地观察。谐波振荡器利用薛定谔方程导出了波函数和谐振子方程。这里有一个问题，蹦极的动作是什么样的?